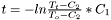Freezer
[Residential loads (residential)]

The freezer model is based on performance profile that can specified by a tape and using a method developed by Ross T. More...

Detailed Description

The freezer model is based on performance profile that can specified by a tape and using a method developed by Ross T.

Guttromson

Original ODE:

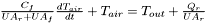
$\frac{C_f}{UA_r + UA_f} \frac{dT_{air}}{dt} + T_{air} = T_{out} + \frac{Q_r}{UA_r}$

where

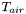$T_{air}$ is the temperature of the water

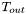$T_{out}$ is the ambient temperature around the freezer

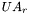$ UA_r $ is the UA of the freezer itself

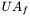$ UA_f $ is the UA of the food-air

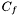$ C_f $ is the heat capacity of the food

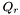$ Q_r $ is the heat rate from the cooling system

General form:

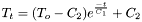
$T_t = (T_o - C_2)e^{\frac{-t}{C_1}} + C_2$

where

t is the elapsed time

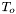$ T_o $ is the initial temperature

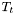$ T_t$ is the temperature at time t

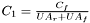
$C_1 = \frac{C_f}{UA_r + UA_f}$

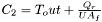
$C_2 = T_out + \frac{Q_r}{UA_f}$

Time solution

$t = -ln\frac{T_t - C_2}{T_o - C_2}*C_1$